大手塾が公開している偏差値表は、模試でその偏差値を取っていれば該当する入試での合格可能性が80%であるとされる値をまとめたものです。また、合格可能性50%の偏差値表も存在します。
これらは多くの受験家庭が強く参考にしている重要な指標ですが、その具体的な算出方法は公開されていません。
そこで、日能研およびSAPIXの入試報告会で配布された入試結果データをもとに、その算出方法を推測しました。以降の内容には断定的な表現を含む場合がありますが、推測が含まれている点にご留意ください。
サンプルデータ
説明のためのサンプルデータは、受験者数250人、合格者数100人とし、持ち偏差値と合否を正規分布に従う乱数を用いて作成しました。
下図の通り、サンプル数が250人でも予想よりきれいな正規分布にはなりませんでした。
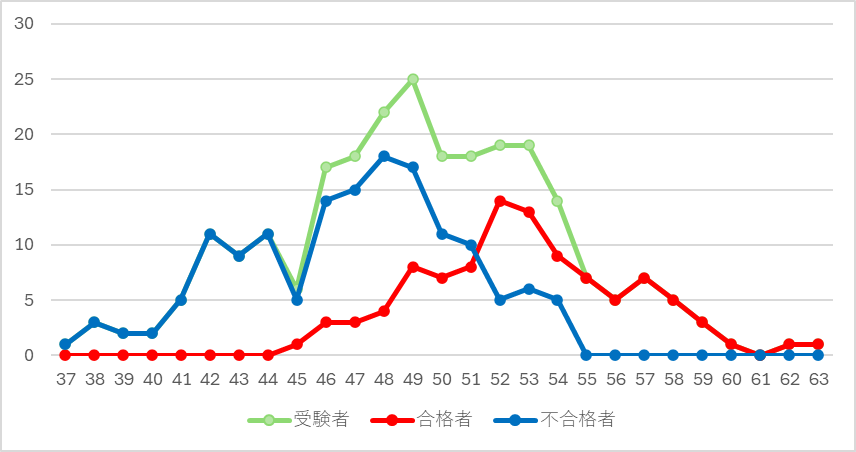
表
| 持ち 偏差値 | 受験者数 | 合格者数 | 不合格者数 |
| 63 | 1 | 1 | 0 |
| 62 | 1 | 1 | 0 |
| 61 | 0 | 0 | 0 |
| 60 | 1 | 1 | 0 |
| 59 | 3 | 3 | 0 |
| 58 | 5 | 5 | 0 |
| 57 | 7 | 7 | 0 |
| 56 | 5 | 5 | 0 |
| 55 | 7 | 7 | 0 |
| 54 | 14 | 9 | 4 |
| 53 | 19 | 13 | 5 |
| 52 | 19 | 14 | 5 |
| 51 | 18 | 8 | 10 |
| 50 | 18 | 7 | 11 |
| 49 | 25 | 8 | 17 |
| 48 | 22 | 4 | 18 |
| 47 | 18 | 3 | 15 |
| 46 | 17 | 3 | 14 |
| 45 | 6 | 1 | 5 |
| 44 | 11 | 0 | 11 |
| 43 | 9 | 0 | 9 |
| 42 | 11 | 0 | 11 |
| 41 | 5 | 0 | 5 |
| 40 | 2 | 0 | 2 |
| 39 | 2 | 0 | 2 |
| 38 | 3 | 0 | 3 |
| 37 | 1 | 0 | 1 |
| 合計 | 250 | 100 | 150 |
SAPIX
偏差値算出方法
SAPIXでは、偏差値帯ごとに合格率を算出し、その値が特定の基準(80%、50%)に達する地点を入試偏差値としていると考えられます。多くの方が「このように算定しているのでは」と想定していた方法に近いのではないでしょうか。
各種資料から、偏差値帯は2刻みで区切って算出していると推測されます。
サンプルデータを偏差値2ごとに区切って合格率を算出すると下図のようになり、80%偏差値は55、50%偏差値は51となります。
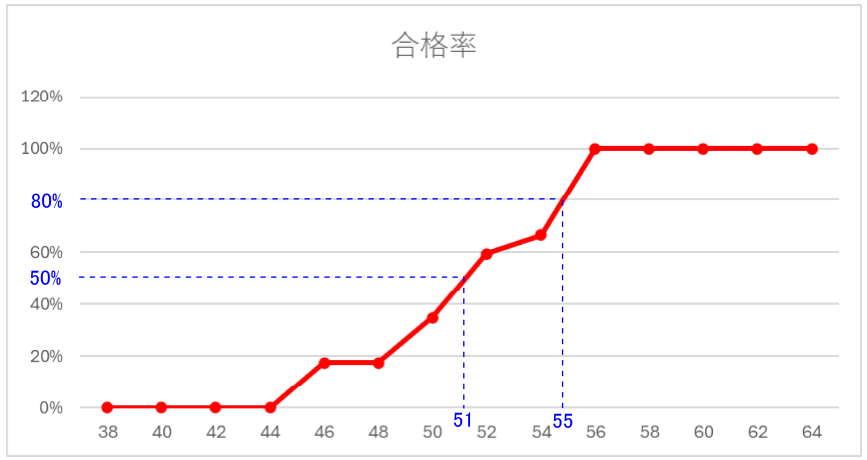
表
| 持ち 偏差値 | 受験者 | 合格者 | 合格率 |
| 64 | 1 | 1 | 100% |
| 62 | 1 | 1 | 100% |
| 60 | 4 | 4 | 100% |
| 58 | 12 | 12 | 100% |
| 56 | 12 | 12 | 100% |
| 54 | 33 | 22 | 67% |
| 52 | 37 | 22 | 59% |
| 50 | 43 | 15 | 35% |
| 48 | 40 | 7 | 18% |
| 46 | 23 | 4 | 17% |
| 44 | 20 | 0 | 0% |
| 42 | 16 | 0 | 0% |
| 40 | 4 | 0 | 0% |
| 38 | 4 | 0 | 0% |
メリット・デメリット
SAPIX方式の利点は、この偏差値を超えていれば合格可能性が〇%以上であることが明確に示される点です。
一方で、偏差値帯を細かく区切って算出する特性上、この方法で入試偏差値の精度を高めるには多くのサンプル数が必要となります。
不足している入試回に関しては、過去の結果を加算して算定するなどの処理が行われている可能性が高いと考えられます。
日能研
偏差値算出方法
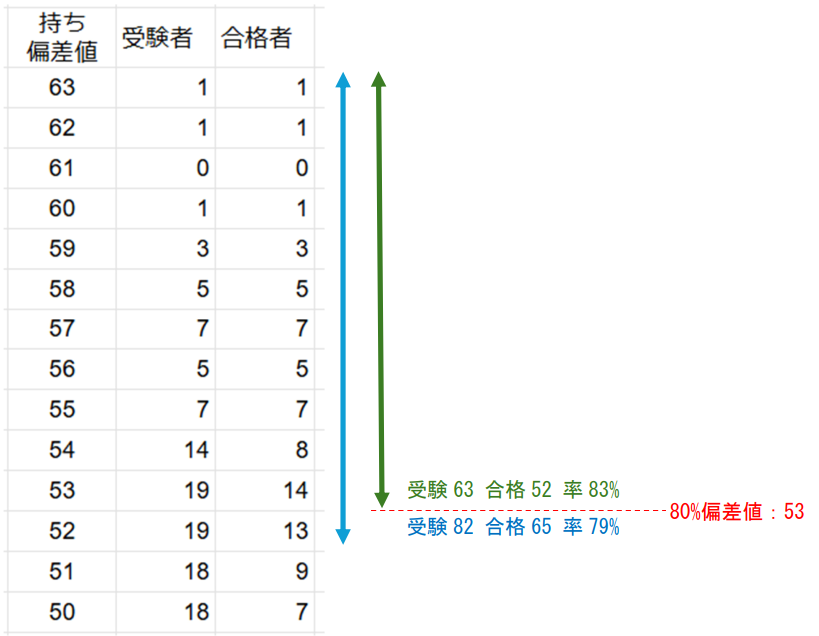
日能研の80%偏差値(R4偏差値)は、持ち偏差値が高い受験生から順に受験者数と合格者数の累計を算出し、合格率が80%となる位置を基準に算定していると考えられます。下図の通り、サンプルデータにおけるR4偏差値は53となります。
ここで、偏差値53の受験生の合格率は 14/19 = 0.74(74%)となっており、80%を下回っている点に注意が必要です。
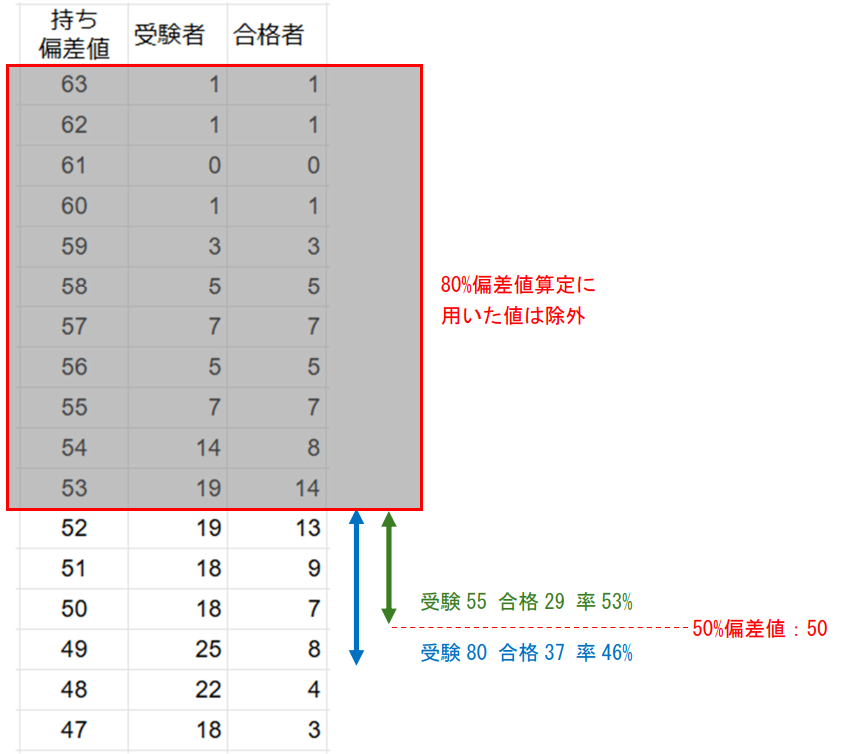
日能研の50%偏差値(R3偏差値)は、80%偏差値を算出する際に用いたデータを除いたうえで、同様の方法で算出していると考えられます。サンプルデータにおけるR3偏差値は50となります(下図参照)。また、SAPIX方式と比較すると数ポイント低い値が算出されます。これは80%偏差値も同様です。
メリット・デメリット
日能研方式の利点は、比較的サンプル数が少なくても入試偏差値を算出できる点です。この集計方法を採用しているため、入試期間後にその年の結果偏差値表を作成・公開することが可能になっていると考えられます。(追記2025/4/1:SAPIXでも結果偏差値が公開されました。今年から?)
一方で、デメリットとしては、80%偏差値ちょうどの受験生の合格率が80%未満となる点が挙げられます。今回のサンプルデータでは大きな影響は見られませんでしたが、受験者の持ち偏差値が正規分布しておらず、上位層に偏っている場合、80%偏差値がかなり低く算出されることになります。
前受け最上位校の栄東A(東大)や渋谷教育学園幕張①ではこの現象が顕著に見られます。また、他の学校でもR3偏差値とR4偏差値の差がわずか1しかない入試回では、同様の現象が起こっている可能性が高いです。その場合、R4偏差値ちょうどでの合格率は80%ではなく50%程度となっていることも考えられます。
補足・まとめ
SAPIX、日能研の入試偏差値算出方法に関して限られた情報からですが推測しました。
特に日能研のR4偏差値は満足していても安全圏でないこともある、ということに注意が必要です。
今回のサンプルデータは正規分布に従う乱数で作成したため、それなりにきれいな結果が出ました。しかし配布されたデータを見ると、どの偏差値帯を取っても合格率が80%を超えない、低い偏差値帯の方が合格率が高い、といった現象が例外と言えないほど頻繁に起こっているのが確認できます。
そういった場合は「なにかしらの操作」を行って入試偏差値を決定しているものと思われます。
いずれの方法でも、統計学的に信頼できる値を得るために必要なサンプル数が、多くの入試回において不足していると考えられます。偏差値表は、合格者が少ない学校では数ポイント程度の誤差が生じる場合があるため、その点を前提に参考にするのが良いでしょう。






